
Jacob Siefert
Graduate Research Assistant
jas7031 (at) psu (dot) edu
Research Interests: Control Systems, Optimal Control, Optimization, Hierarchical Control, Reachability Analysis, Model Predictive Control
Education:
- M.S. Mechanical Engineering – University of Minnesota (June 2021)
- B.S. Mechanical Engineering – University of Maryland (Dec. 2016)
Research
Current (PSU): Reachability analysis, model predictive control, hierarchical control, thermal management & electrical systems, hybrid systems
Previous (UMN): Optimal control, constrained optimization, hybrid hydraulic-electric systems, and control over discrete operating decisions
Research by Jacob Siefert, Ph.D. Student:
Reachable and invariant sets are used to evaluate system performance and ensure constraint satisfaction in safety-critical applications while accounting for the effects of input, disturbance, and parameter uncertainties. For discrete-time systems, reachable sets are calculated by recursion over successor sets. For nonlinear systems, the complexity and nonconvexity of successor sets limit the scalability of existing approaches.
To improve scalability of calculating successor sets for nonlinear systems, this approach builds on our previous method for hybrid systems that leveraged hybrid zonotopes and a novel construct called a state-update set. Hybrid zonotopes can represent nonconvex, potentially disjoint sets efficiently by representing the union of an exponential number of convex sets using only a linear number of variables. Hybrid zonotopes are closed and have efficient identities for fundamental set operations including linear transformations, generalized intersections and Minkowski summations. A state-update set encodes all possible state transitions of a dynamic system. Using the state-update set, our work has developed a successor set identity using set operations that are efficient for hybrid zonotopes. The successor set identity and a visual representation of the identity is shown in Fig. 1. An extension to nonlinear systems is achieved by using an over-approximation of the nonlinear state-update set represented using a hybrid zonotope. In doing so, over-approximations of reachable sets are generated with linear memory complexity growth and computational complexity that scales linearly with the number of states.
To generate an over-approximation of the nonlinear state-update set, theoretical techniques to approximate nonlinear functions using Special Ordered-Set (SOS) approximations and bounds on SOS approximation error are leveraged. Our approach then efficiently converts SOS approximations into a hybrid zonotope. Fig. 2 shows a sinusoid (green), an SOS-approximation (red), and an over-approximation of the sinusoid (blue) represented as a hybrid zonotope.
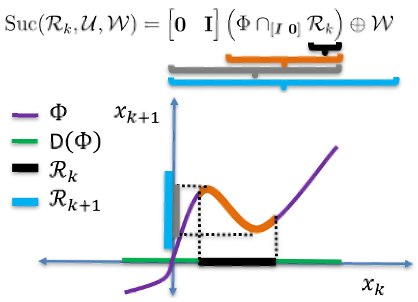
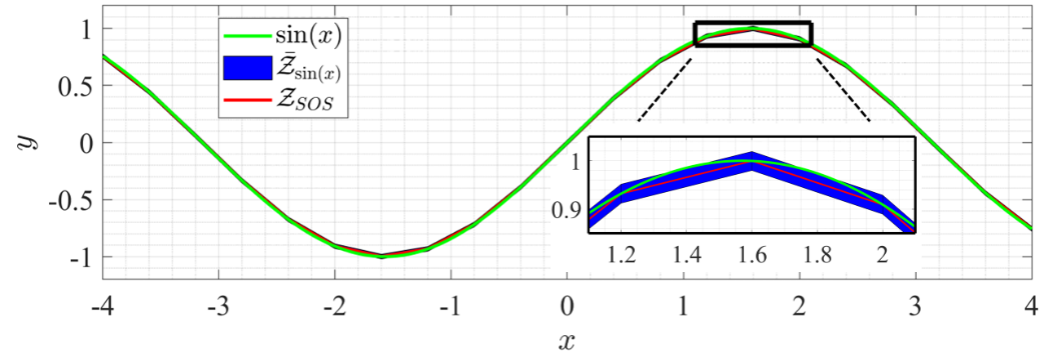
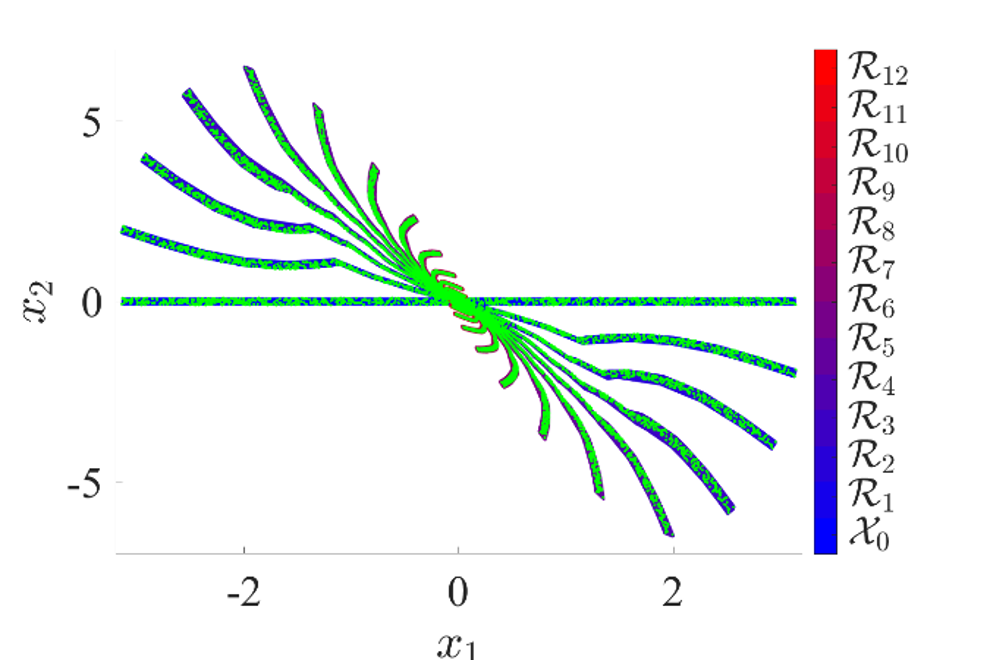
Fig. 3 shows reachable sets generated for pendulum-like dynamics in closed loop with a saturated feedback controller. Exact trajectories from randomly sampled initial conditions (green) are also plotted. As the reachable set is never significantly removed from sampled trajectories, it is shown that the over-approximation captures the nonlinear dynamics well, without excessive conservatism.
Research by Jacob Siefert, Ph.D. Student:
Reachable and invariant sets are used to evaluate system performance and ensure constraint satisfaction in safety-critical applications while accounting for the effects of input, disturbance, and parameter uncertainties. For discrete-time systems, reachable sets are calculated by recursion of precursor and successor sets.
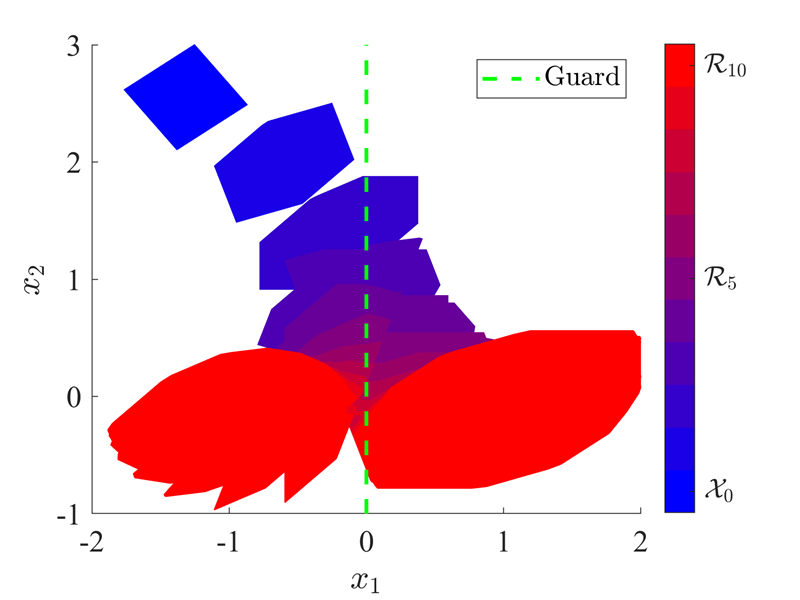
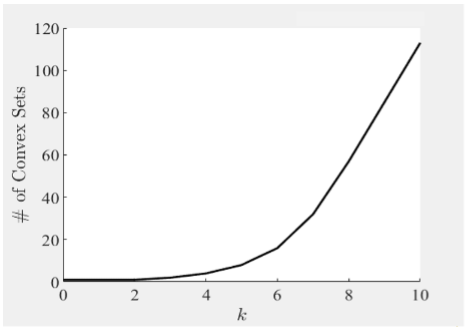
Problem: For hybrid systems with continuous and discrete dynamics, the complexity and non-convexity of precursor and successor sets limit the scalability of existing approaches. This is demonstrated using a numerical example for a piecewise affine system with only two regions separated by a so-called guard. Using convex approaches at each time step, reachable sets are partitioned along the guard and the appropriate affine dynamics are applied to each region. The guard and reachable sets are plotted in Fig. 1 starting from the set Xo. The number of convex sets for each time step is plotted in Fig. 2. The process of partitioning set results in more than 100 convex sets in only 10 time steps. In general, this process may result in the number of convex growing exponentially with time, significantly limiting the number of time steps over which analysis can be performed.
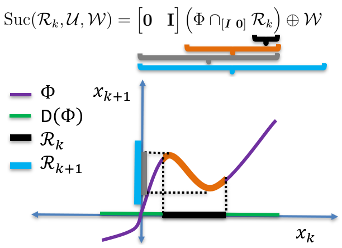
Method: To improve scalability of calculating successor and precursor sets, our approach combines a novel set representation called the hybrid zonotope with a novel construct called a state-update set. Hybrid zonotopes can represent nonconvex, potentially disjoint sets efficiently by representing the union of an exponential number of convex sets using only a linear number of variables. Hybrid zonotopes are closed and have efficient identities for fundamental set operations including linear transformations, generalized intersections and Minkowski summations. A state-update set encodes all possible state transitions of a dynamic system. Using the state-update set, our work has developed successor and precursor sets identities using set operations that are efficient for hybrid zonotopes. The successor set identity and a visual representation of the identity are shown in Fig. 3.
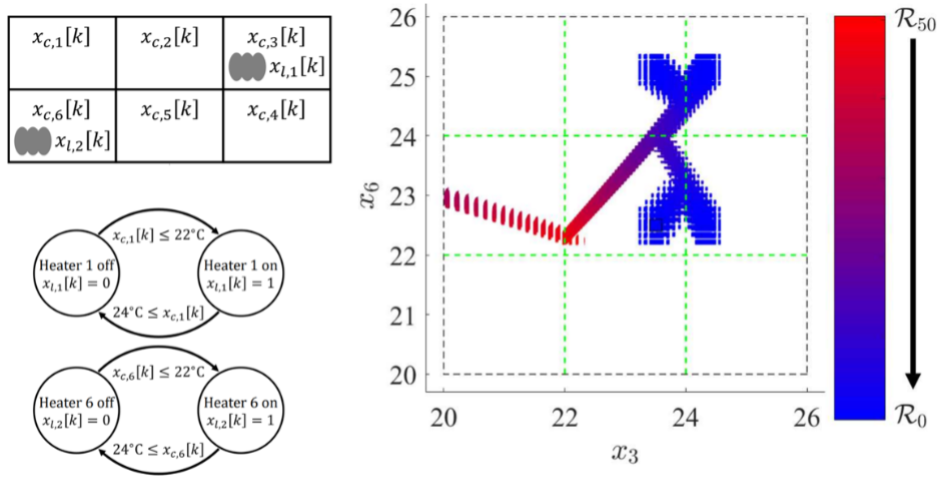
Results: Numerical results demonstrated the improved scalability of the approach over the state-of-the-art, reducing the memory complexity growth from exponential to linear. One numerical result compared the proposed approach and the state-of the-art for a room heating example with six rooms and two heaters. The room layout, heater on/off logic, and 50 backwards reachable sets from R50 are shown in Fig. 4. The proposed approach took 0.34 seconds to calculate while the state-of-the-art took over 202 seconds, resulting in the proposed approach being nearly 600 times faster. The proposed approach also resulted in a memory complexity 1/60th that of the state-of-the-art.
Research by Jacob Siefert, Ph.D. Student:
Set-based reachability analysis calculates all trajectories of a dynamic system subject to uncertainties in its initial condition, inputs, disturbances, and/or model. This analysis can be used to guarantee performance and constraint satisfaction of safety-critical systems, often by showing that reachable sets do not intersect unsafe regions. Exact reachable sets grow in complexity with time, becoming more computationally demanding to compute and requiring more memory to store. Established techniques (e.g., Interval Hull (IH-method) and Cascade Reduction (CR)) reduce exact reachable sets to lower-order approximations but are limited to discrete-time linear time-invariant (LTI) dynamics (for IH-method) or only guarantee that approximation error is bounded by an unknown exponential function (for CR). This research has developed a generalized over-approximation algorithm for computing reachable sets of discrete-time linear time-varying (LTV) dynamics, named DRAWBES, that leverages set representation to guarantee explicit error bounds. Furthermore, a periodic implementation of DRAWBES, DR-PPB, demonstrates that DRAWBES reduces over-approximation error AND computation time as compared to existing methods, while also providing explicit error bounds.
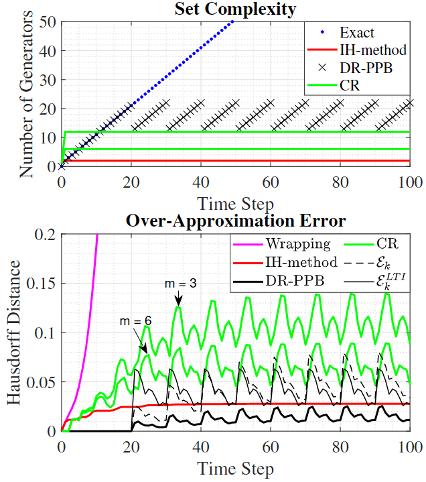

Fig. 1 compares set complexity and over-approximation error for exact and over-approximation methods, while Fig. 2 compares computation times. Exact reachable set complexity grows unbounded, while approximation methods exhibit bounded complexity. A key contribution is that DRAWBES produces explicit error sets, ε_k and ε_k^LTI, that bound the over-approximation error. The distinction between these two error sets is that ε_k^LTI can be pre-computed prior to reachability analysis but is limited to LTI dynamics, whereas ε_k must be computed online but is valid for LTV dynamics. As shown on the lower subplot of Fig. 1, these error sets provide upper bounds on the over-approximation error of DR-PPB, which itself has the least error of any method. As shown in Fig. 2, computation times for exact method grow super-linearly with the number of time steps taken, while approximation methods grow linearly. DR-PPB has tuning parameters that can be adjusted to balance over-approximation error, set complexity, and computation time. For the choice of tuning parameters in this case study, DR-PPB has higher set complexity than the existing methods but avoids performing over-approximations at every time step, resulting in the lowest computation time.
Publications
- J. Glunt, J. Siefert, A. Thompson, H. Pangborn, “Error Bounds for Compositions of Piecewise Affine Approximations,” 2024. [arXiv]
- J. Siefert, T. Bird, A. Thompson, J. Glunt, J. Koeln, N. Jain, H. Pangborn, “Reachability Analysis Using Hybrid Zonotopes and Functional Decomposition," 2024. [arXiv]
- T. Bird, J. Siefert, H. Pangborn, N. Jain, "A Set-based Approach for Robust Control Co-design", 2023. [arXiv]
- J. Siefert, A. Thompson, J. Glunt, H. Pangborn, “Set-valued State Estimation Using Hybrid Zonotopes," IEEE Conference on Decision and Control, 2023.
- Glunt, J.J., Siefert, J.A., Pangborn, H.C., Brennan, S.B., "Challenges in Integrating Low-level Path Following and High-level Path Planning Over Polytopic Maps", Modeling, Estimation and Control Conference, 2023.
- J. Siefert, T. Bird, J. Koeln, N. Jain, H. Pangborn, “Successor Sets of Discrete-time Nonlinear Systems Using Hybrid Zonotopes,” American Control Conference, 2023.
- J. Siefert, T. Bird, J. Koeln, N. Jain, H. Pangborn, “Robust Successor and Precursor Sets of Hybrid Systems Using Hybrid Zonotopes,” IEEE Control Systems Letters, 2022. (jointly submitted to IEEE Conference on Decision and Control)
- J. Siefert, D. Leister, J. Koeln, H. Pangborn, "Discrete Reachability Analysis with Bounded Error Sets", IEEE Control Systems Letters, 2022. (jointly submitted to American Control Conference)
- J. Siefert, P. Y. Li, "Optimal Control of the Energy-Saving Hybrid Hydraulic-Electric Architecture (HHEA) for Off-Highway Mobile Machines", IEEE Transactions on Control Systems Technology, 2021.
- A. Khandekar, J. Siefert, P. Y. Li, "Co-Design of a Fully Electric Hybrid Hydraulic-Electric Architecture (FE-HHEA) for Off-Road Mobile Machines", American Controls Conference, 2021.
- J. Siefert, P. Y. Li, "Optimal control and energy saving analysis of common pressure rail architectures: HHEA & STEAM", BATH/ASME Symposium on Fluid Power and Motion Control, 2020.
- J. Siefert, P. Y. Li, "Optimal operation of a hybrid hydraulic-electric architecture for off-road mobile machines over discrete operating conditions", American Controls Conference, 2020.
- P. Y. Li, J. Siefert, "A hybrid hydraulic-electric architecture (HHEA) for high power off-road mobile machines", BATH/ASME
Symposium on Fluid Power and Motion Control, 2019.

